Редове на Лоран изолирани единични точки и тяхната класификация. Изолиране на особени точки, тяхната класификация. Значение на особени точки

точка

по математика.

1) Точката на кривата, приписана на линиите F ( x, y) = 0, - точка M 0 ( x 0, y 0), По същия начин частните лоши функции F ( x, y) Обратно към нула:

Поради тази причина не всички други частни случайни функции F ( x, y) В точката M 0, равна на нула, тогава O. t. Тъй като редът на първите отиващи към нула в точката M 0 отиват на нула и всички останали отиват на нула, а не всички трети отиват на нула, тогава O. t. При по-нататъшно изкривяване наблизо подводното течение на О. т. Важна роля играе знакът на

Ако Δ> 0, тогава O. t. се нарича изолиран; например при криви y 2 - x 4 + 4x 2\u003d 0 кочана на координатите е изолиран O. t. (Div. Мал един ). Yakscho Δ x 2 + y 2 + a 2) 2 - 4a 2 x 2 - a 4\u003d 0 кочан от координати є wuzlov O. t. (Div. Мал 2 ). Ако Δ \u003d 0, тогава O. t. dotic y 2 - x 3= 0 (дел. Мал 3 , а); б) повратна точка от 2-ри вид - различни игли с криви шевове от едната страна под формата на точка, като крива (y - x 2)2 - х 5= 0 (дел. Мал 3 , B); в) точка на самоконтакт (за крива y 2 - x 4= 0 кочанът на координатите е точката на самоконтакт; (Div. Мал 3 , V). Редът на обозначенията на O. t. например, асимптотична точка е върхът на спирала с безкраен брой завои (div. Мал 4 ), точка на закрепване, точка на върха и т.н.

2) Специална точка на диференциалното подравняване е точка, в която цифровото циферблат и еталонът на дясната част на диференциалното подравняване (Div. Differential alignment) се обръщат на нула едновременно

de Р і Q - непрекъснато диференциращи функции. Като оставите O. t. Roztashovanoy върху кочана на координатите и використката формула на Тейлър (Div. Taylor formula), можете да видите подравняването (1)

де P 1 ( x, y) I Q 1 ( x, y) - безкрайно малък по отношение на възрастта до

Същото нещо, λ 1 ≠ λ 2 i λ 1 λ 2> 0 или λ 1 = λ 2, тогава O. t. всички интегрални криви, които преминават през точките, за да достигнат до малките покрайнини на възела, влизат в новия. Ако λ 1 ≠ λ 2 i λ 1 λ 2 i β, α ≠ 0 i β ≠ 0, тогава O. t. Є фокус; всички интегрални криви, които преминават през точките, за да достигнат до малката периферия на фокуса, са спирали с безкраен брой завои във все по-малката периферия на фокуса. Якшчо, нареши, λ 1,2 = ± иβ, β ≠ 0, тогава характерът на O. t. x, y) I Q ( x, y); тук O. t. може да бъде фокус или център, или майка и по-сгъваем характер. В близост до центъра всички интегрални криви са затворени и центърът е в средата на себе си. Така, например, точката (0, 0) е възел за равен в" = 2г/х(Λ 1 = 1, λ 2 = 2; раздел. Мал 5 , А) и г" = г/х(Λ 1 = λ 2 = 1; раздел. Мал 5 , B), седло за изравняване y"=-y/z(Λ 1 = -1, λ 2 = 1 ; см. Мал 6 ), фокус за изравняване y "=(х + у) / (х - у) (Λ 1 = 1 - и, Λ 2 = 1 + и; см. Мал 7 ) Центрирам за изравняване y"=-x/y(Λ 1 = -i, Λ 2 = и; см. Мал осем ).

Yakscho x, y) и Q ( x, y) Аналитичен, около O. t. В по-висок ред може да бъде разделен на области: D 1 - изпълнени с интегрални криви, двата края са включени в O. t. (параболични области), и D 3 - области, заобиколени от две интегрални криви, които са включени в O. t. Мал 9 ). Тъй като няма интегрални криви, които влизат в O. t., тогава O. t. се нарича точка от стабилен тип. Заобиколен от стабилен O. t. Развива се от затворени интегрални криви, които отмъщават O. t. Мал 10 ).

Vivchennya O. t. Differential rivnyan, т.е. по същество развитието на поведението на семейства от интегрални криви в близост до O. t. M. Lyapunov a, A. Poincaré et al.).

3) Единствена точка на еднозначна аналитична функция е точка, в която аналитичността на функция е нарушена (раздел. Аналитични функции). Yakshcho іsnuє близо до O. t. а, Vіlna vіd іnshih O. t., тогава точката анаричат ​​изолиран О. т. Якшчо а- изолиран О. т. е(а)= b, Можете да получите какво астане основната точка на коригираната функция. Например, точка z\u003d 0 є приет O. t. За функцията f 1 ( z) = е(z), Якчо z≠ 0, і е 1(0),=1, точка z= 0 е 1 (z) Аналитичен до точката z= 0]. yakscho а- изолиран O. t. I и наречен полюс или не специална точка на функция е(z), както и серия Лоран). е(z) В близост до изолирани О. т. Не отмъщавайте за отрицателни стъпки z - a, като а- търсене на О. т. z - a, като а- полюс (когато реда на стълба Р vynachaetsya като най-важните стъпки и - istotno специална точка. Например за функцията

p = 2, 3, ...)

пъстър z= 0 є полюсен ред Р, За функция

пъстър z= 0 е точно особена точка.

На кордона на кладата на държавната линия е виновен, че е приел един О. т. Всички гранични точки на района се основават на еднозначна аналитична функция (естествен кордон) - O. t. И така, всички петна от един кол | z| = 1 є специално за функцията

За една богато смислена аналитична функция концепцията за „Относно Т.“ е по-последователна. Krim O. t., В другите дъги на риманова повърхностна функция (тоест O. t. на еднозначни аналитични елементи), дали точката на разделяне също е O. t. Functions. Изолирането на точките на разделяне на риманова повърхност (тоест точките на разделяне на риманова повърхност, които в deakіy їх покрайнини и в една арка няма други O. t. Функции) се класифицират като офанзивен ранг. Yakshcho a - изолираната точка на разделяне на терминалния ред и главния терминал a се нарича критичен полюс. yakscho а- изолираната точка на отделяне на непростим ред и се нарича трансцендентна O. t. Всички други изолирани точки на отделяне се наричат ​​критични и сингулярни точки. Приложете: точка z= 0 е крайната критична точка на функцията f ( z) = Ln zи критично уникална точка на функцията е (z) = Дневник на греха z.

Be-yak O. t., Krіm usunenoy, є pereskoda с аналитични prodovzhennі, т.е. Analytical prodovzhennya vzdovzh крива, scho да премине през неизбежната O. t., Невъзможно.

Голяма Радианска енциклопедия. - М .: Радианска енциклопедия. 1969-1978 .

Чудите се какво е "Специална точка" в други речници:

Покажи ми тук. Раздел. Това също е специална точка (диференциално подравняване). Сингулярност или сингулярност в математиката е точка, в математически обект (назовете функция) няма присвояване или може да има неправилно поведение (например точка в ... ... Уикипедия

Аналитичните функции са точка, в която умът на аналитичността е разбит. Като такава, аналитичната функция f (z) е дадена във вътрешната околност на точка z0 навсякъде ... физическа енциклопедия

Точка на аналитичните функции, в която аналитичността на функцията е разрушена ... Страхотен енциклопедичен речник

точка- - [Я.Н.Лугински, М.С.Фези Жилински, Ю.С.Кабиров. Английско-руски речник по електротехника и енергетика, Москва, 1999] Теми в електротехниката, основни понятия EN единствена точка ... Технически превод Dovіdnik

1) O. t. Аналитична функция f (z) на прехода за аналитичното продължение на елемента от функцията f (z) на комплексния zminny z по произволен път в областта на zminny. Нека аналитичната функция f (z) бъде приписана на декана ... ... математическа енциклопедия

Аналитични функции, точка, в която аналитичната функция е нарушена. * * * СПЕЦИАЛНА ТОЧКА СПЕЦИАЛНА ТОЧКА на аналитична функция, точка, в която аналитичността на функция се нарушава ... енциклопедичен речник

точка- ypatingasis taškas statusas T sritis automatika atitikmenys: engl. единствена точка вок. единствено число Punkt, m рус. специална точка, f pranc. точкова частица, m; точка singulier, m ... Automatikos terminų žodynas

Редовете на Тейлър служат като ефективен инструмент за разработване на функции, аналитични в числото zol. За допълнителни функции, аналитични в областта на пръстена, е възможно да се разширят положителни и отрицателни стъпки (z - zq) под формата на значително разширение на Тейлър. Ред (1), който се разбира като сбор от два реда, се нарича ред на Лоран. Ясно е, че площта на кожата на реда (1) е горната част на участъците от кожата на редовете (2). Ние я знаем. Площта на ефективност на първия ред, т.е. радиусът на който се приписва на формулата на Коши-Адамар. Другата серия е статична серия от произволно променящ се ред (5), за да се сближи в средата на своя залог към аналитичната функция на комплексното променящо се m- * oo ) є zvnіshnіst kol - Yakshko, който іsnuє zagalna площ zbіzhnostі ryadіv (3) і (4) - кръгов пръстен в яком ред (1) се доближават до аналитична функция. В случай на tsimu във всеки случай kіltsi, vіn се сближават абсолютно и еднакво. Пример 1. Определете областта на сближаване на редицата на Лоран Изолирани особени точки и тяхната класификация M функцията f (z), недвусмислена и аполитична в кръгова Котчи, може да се види във всяка окръжност, ако сте в състояние да се сближите до серия на коефициентите Sp, които са еднозначно зададени и се изчисляват по формулите de 7p - около радиуса m Нека разгледаме кръговете като центрове в точката, чиито радиуси удовлетворяват неравномерността и да разгледаме новия пръстен. За интегралната теорема на Коши за многосвързана област е възможно да се съгласува кожата с интегралите в сбора (8 ). За всички точки £ от числото 7d * concurrency de sumi се сближават равномерно към редицата 1 + 1. За всички точки £ на окръжността ir> можем да си представим, че drib ^ може да си представим, че редът може да се види, че се сближава еднакво. функциите във формули (10) и (12) са аналитични функции в кръгов кръг. Следователно, по силата на теоремата на Коши, стойностите на дадените интеграли не се променят, така че заменете кръговете 7 / g и 7 g / да бъде окръжност. Tse ви позволява да комбинирате формули (10) и (12), като замените интегралите в дясната част на формулата (8) с вирази (9) и (11) поредицата (14) се сближава до функцията f (z) навсякъде във всяка окръжност, освен това във всяка окръжност редът се сближава до функцията f (z) абсолютно и еднакво. Довеждаме сега, че разположението на ума (6) е същото. Да приемем, че може да има още едно място Тоди навсякъде в средата на пръстена R matimemo. По обиколката на реда (15) се сближават равномерно. Умножете нарушената част от равенството (de t е фиксирано цяло число и интегрираме редовете с нарушение член по член. В резултат на това изваждаме в лявата част, а в дясната част - SS. И така, поредицата ( 6), чиито коефициенти се изчисляват по формула (7), се нарича ред на Лоран на функцията f (z) в кръга.Формули (7) за коефициентите в реда на Лоран се използват рядко на практика, но, като правило, те включват тромави изчисления.същият резултат. тром в точка = 0. в кожни функции / (г) е аналитичен: Известно е лаурентовото разпределение на функциите / (z) в кожата на тези области. Да вземем / (z) за сумата от елементарни дроби a) Colo Reversible spіvvіdnoshennia (16) нека подходим към формулата за сумата от членове в геометрична прогресия, като вземем предвид знанието за разширението във формулата (17): б) Пръстенът за функцията -p е изпълнен със сходящи се в същия пръстен, така че серия (19) за функцията j ^ j с | z | > 1 за разпръскване. Следователно преобразуваме функцията / (z) в следващия ред: Повтарям формулата (19), вземаме предвид, че редът се сближава за. Замествайки оформлението (18) и (21) в spіvvіdnoshennia (20), то се приема в) Извикване на залог за функцията -р при | z | > 2 се разминават и ред (21) за функцията<*> Vykoristovuyuchi формули (18) и (19), otrimaєmo ABO 1 Неговото дупе показва, че за една ієї і tієї w функции ї f (z) Лоран оформление, vzagali изглежда, може да изглежда различно за различните градове. Задница 3. Значителен Rycladdan 8 Row на Laurent Funkії Ryadi Lorana izolovіkatiy и Kіltsevo и SchoristaєMosia и Kіltsevo и SchoristaєMosy AM до Funky Funki F (z) In the Assurance Visigands: І Recalimately Друг Dodaocks Formula Vicorovy Член за Suchimi Progressive 22), може да се приложи 4. Изложете в серия на Лоран функцията в близост до тънък zq = 0. за всяка сложна точка z - 0. Областта на Qiu може да бъде причислена към предстоящото спiввидене: Тази функция е аналитична в областта на H формули (13) за коефициентите в серия на Лоран със същите mikrkuvanniami, shcho і в предния параграф, можете да премахнете неравностите на Kouiw. ако функцията f (z) е описана върху окръжността, de M е постоянна), то изолираните особени точки Точката zo се нарича изолирана сингулярна точка на функцията / (z), тъй като тя има централния кръг на точката която функция f (z) е еднозначна и аналитична. В самата точка zo функцията или не е назначена, или не е еднозначна и аналитична. В зависимост от поведението на функцията / (d), при приближаване до точката zo се разграничават три типа конкретни точки. Изолирана точка на сингулярност се нарича: 1) изолирана сингулярна точка, така да се каже, 2) изолирана особеност, като 3) сингулярна особена точка, тъй като функцията f (z) не може да бъде между at go. Теорема 16. Сингулярната точка z0 на функцията f (z) се изолира от особена точка, в този случай, само в обратната посока, ако разширението на Лоран на функцията f (z) в околността на точката zo прави не отмъщава главата част, т.е. изброяване единична точка. Следователно функцията f (z) е заобиколена от прокологична съседство на функциите на точка th / (d) в близост до точка zq, може да се види само правилната част, т.е. . Няма значение дали при z - * z0 Функциите / (r) имат гранична стойност: Теорема 17. Точката zq на функцията f (z) е изолирана, особено ако се използва само ако функцията J (z) е заобиколена от реални пробити покрайнини на точка zq, Zgmechaі ні. Да тръгваме - точката на функцията / (r) е изчерпателна. Важно е да се отбележи, че функцията /(r) е аналитична в другата посока с център в точката. Tse vyznaє име на точката - изброяване. Теорема 18. Една единствена точка zq на функцията f (z) се изолира като полюс в това и само в този случай, ако главната част на Лорановото разширение на функцията f (z) в околността на точката има крайно (и положително) числено различни членове от нулеви членове, т.е. 4 Нека z0 - полюс. И така, като се пробива точката z0, в която функцията f (z) е аналитична и подобна на нула. Тогава в кръга се задава аналитичната функция, освен това Otzhe, точката zq е особената точка (нула) на функцията, или h (z) е аналитична функция, h (z0) Ф 0. Тогава функцията е аналитична и h (zo) Ф 0, то функцията w е аналитична в околността на точка zq, а също така е възможно функцията f (z) да се намери в пробитата околност на точка z във вида ( 24). Tse означава, че в тази околност функцията f (z) е аналитична едновременно с функцията. За функцията g (z) е справедливо да се покаже, че zq е особена точка на функцията g (z) и същата функция при 0 pragne е полюсът на функцията Може да има друг прост факт. Точката Zq е полюс на функцията f (z) в това и само в този случай, ако функцията g (z) = y може да бъде разширена до аналитична функция в близост до точката zq, като се зададе g (z0 ) = 0. Извиква се редът на полюса на функцията f (z) порядъкът на нула на функцията jfa. От теореми 16 и 18 началото на твърдостта е вибриращо. Теорема 19. Изолирана особено тънка - точно единична в това и само в този случай, ако главната част на Лаврентийското оформление в пробитите покрайнини на центъра на точката отмъщава безкрайно богата на нулеви членове. Пример 5. Сингулярна точка на функцията ї zo = 0. Ред на Мей Лоран Изолиране на особени точки и их класификация Otzhe, zo = O - изброяване особена точка. Разширяването на функцията / (z) в серия на Лоран в близост до нулевата точка, за да покрие само правилната част: Пример7. / (G) = Специална точка на функцията f (z) є zq = 0. Можем да разгледаме поведението на функцията върху осите на делене и изричната ос: върху оста на делене при x 0, върху изричната ос Otzhe, nі терминал, nі безкрайна граница f (z) при z - * 0 не е валидно. И така, точката th = 0 е абсолютно особена точка на функцията f(z). Знаем лорентиевото разширение на функцията f (z) в околността на нулевата точка. За какъвто и да е комплекс Z може да бъде Poklademo. За да повторим разширението на Лорентиан, има безкраен брой членове с отрицателни стъпки z.

Назначаване.Извиква се особена точка на функция изолиран, yakscho в точката deakіy okolitsі tsієї - аналитична функция (така че е аналитична в ринга).

Класификацията на изолирани особени точки на функция е свързана с поведението на функцията в близост до особена точка.

Назначаване.точка се нарича usunennoy специална точка на функция, сякаш е последната граница между функциите в.

Пример 5.Покажете, че функцията може да бъде единична в точката на изброяване.

Решение.Згадуючи първата чудотворна граница, изчислима

Така че в момента функцията е настроена да има сингулярност на търсене.

Задача 4.Покажете за какво служи точката за изброяване.

Назначаване.точка се нарича полюс функции, така че функцията да не е ограничена от растеж, когато, tobto.

Zvernemo уважение към връзката между разбиранията за нула и полюсите на аналитичната функция. Нека премахнем функцията на зрителя.

Ако точката е проста от нулата на функцията, тогава функцията може да бъде в обикновен полюс

Ако точка е нулев ред за функция, тогава за функция тя е полюс поръчка.

Пример 6.Покажете, че функцията може да бъде в точката на полюса от трети ред.

Решение.Моля те, вземи го. Когато pragnenny до нула s be-всеки закон може. След това и с него самата функция нараства без подобрение. Оттук нататък това е специална точка є полюс. За функция точката, очевидно, е тройна нула. Така че за дадена функция точката е полюс от трети порядък.

Задача 5.Покажете, че в точката има прост полюс.

Назначаване.точка се нарича точно особено точка на функция, въпреки че в тази точка няма крайна, никаква ограничаваща граница на функцията (поведението на функцията не е дефинирано).

Нека това е оригиналната единствена точка на функцията. Тогава за всяко предварително зададено комплексно число има такава последователност от точки, които се сближават до, която е най-важната стойност, до която да се придвижите нагоре: ( теорема на Сохочки).

Пример 7.Покажете, че функцията в точка може да има своя собствена сингулярност.

Решение.Нека разгледаме поведението на дадената функция около точката. Когато положителната част на положителната ос е стеснена (tobto), е възможно; yakscho w uzdovzh отрицателна част на оста deisnoy (tobto), тогава i. Така че, не іsnuє mezhі prі. За целта, в точката на функция, може да има известна особеност.

Нека разгледаме поведението на функцията при нула от гледна точка на теоремата на Сочокки. Хайде - бъди комплексно число, виж нула и несъответствие.

От ревност знаем. Важно е да вземем предвид последователността на точките. Очевидно,. В скин точката на последователност функцията е добра, до това т.е

Задача 6.Покажете, че функцията може да бъде абсолютно същата.

Неясно отдалечената точка винаги се зачита като специална характеристика на функцията. Точката се нарича изолирана особена точка на функцията, тъй като функцията на позицията на залога с център върху кочана на координатите няма други особени точки.

Класификацията на изолираните единични точки може да бъде разширена чрез обрат.

Пример 8.Покажете, че функцията може да бъде върху несъответствието на двуразовия полюс.

Решение.Нека да разгледаме функцията, де-аналитичната функция около точката, освен това. Така че функцията може да бъде върху несъответствието на нулата джудже, но същото за функцията, точката е полюсът на джуджето.

Пример 9.Покажете, че функцията може да бъде неясна и уникална.

Решение.Подобна задача е разгледана в пр.7. Нека разгледаме поведението на функцията в близост до безкрайно далечна точка. Със стесняване на положителната част на динамичната ос и със стесняване на отрицателната част на динамичната ос. Това означава, че няма взаимофункции в точка i, поради зададената точка, тя е абсолютно специална.

За естеството на сингулярността на функцията в точка може да се съди по част на главата Лаврентийско оформление в близост до централната точка.

Теорема 1.За да е точката була usunennoy специална функция, необходима и достатъчна не отмъсти за частта на главата.

Задача 6.Разширяването на функцията на Koristuyuchis Taylor в близост до точката, показва, че може да има сингулярност в нулите.

Теорема 2.За да е точката була полюс функции, необходими и достатъчни, щоб част на главата vydpovidny loranivsky rozladannya mistila kitsev брой членове :

Номерът на най-високия отрицателен член определя реда на полюса.

В кой изглед функцията може да бъде представена в изгледа

de - аналитична по точкова функция, - ред на полюса.

Пример 10.Покажете, че функцията може да бъде в точки и прости полюси.

Решение.Нека разгледаме точката. Нека ускорим Laurentian оформлението на функцията в близост до точката, ще го вземем в приложение 2:

Тъй като в главната част на най-старата (и единица) стъпка на по-старата единица е отрицателна, точката е прост полюс на тази функция.

Можете да приемете резултата по различен начин. Можем да видим и да платим - тази функция е аналитична в точка i. И така, і по силата на (8) в точката, в която функцията е дадена с прост полюс.

Още един начин: нека разгледаме функцията, като обикновена нула в точката. И така, в този момент има обикновен стълб.

По същия начин, ако напишете функция във визуален, de - функция, която е аналитична в точка i, тогава веднага става ясно, че точката е прост полюс на функцията.

Задача 7.Покажете, че функцията има полюс от 2-ри ред в точката и полюс от 4-ти порядък в точката.

Теорема 3.За да е точката була точно особено точка на функция, необходима и достатъчна, шоб част на главата Лаврентийско оформление в близост до точката пропусна неограничен брой членове .

Пример 11.Определете естеството на сингулярността в точката на функция

Решение.Можем да поставим заместител на видимото разпределение на косинуса:

Така че, Laurentian оформление в покрайнините на точката може да изглежда

Тук частта е правилна - един dodanok. И основната част е да отмъстиш за неизчерпаем брой dodankiv, това е смисълът - това е особено специално.

Мениджър 8.Покажете, че в дадена точка функцията може да има своя собствена особеност.

Нека да разгледаме функцията и да запишем нейното Laurentian оформление в точки:

Zrobimo zamіnu, с което точката да отидете на точката. Сега в близост до безкрайно отдалечени точки може да бъде

Изгубен, за да въведе ново определение. приемливо

de - главната част и - правилната част от лаврентовското оформление на функцията в близост до безкрайно далечната точка. По този начин, в Лаврентовото оформление на функциите в близост до точката, главната част е поредица от положителни стъпки, а правилната част е поредица от отрицателни стъпки. Поглеждам назад към мястото

каналите на индуциращи критерии за определяне на естеството на сингулярността вече не са валидни за неопределено отдалечена точка.

Пример 12.Обяснете естеството на сингулярността на функцията до точката. , то в даден момент може да изглежда неизолирано.

Пример 15.Функцията в безкрайно различни точки може да бъде уникална. Покажете, че точката за функцията не е изолирана особена точка.

Решение.Функцията има безлични полюси в нулите на стандарта, тоест в точките. Така че як, тогава точка, в близост до някакъв полюс, є граница за полюсите.

Модели, които се описват от системи от две автономни диференциални линии.

Фазова равнина. Фазов портрет. Изоклинен метод. Изолинии на главата. Стабилност на стационарно състояние. Линейни системи. Видове специални точки: вузол, седло, фокус, център. Пример: химични реакции от първи ред.

Най-добрите резултати на модела на яки за силата на биологичните системи са взети на модели с две диференциални нива, които позволяват шейна за допълнителен метод фазова равнина. Нека да разгледаме системата от две автономни първични диференциални равни в глобален изглед

(4.1)

P(x, y), Q(x, y)- непрекъснати функции, назначени в активната зона гевклидова равнина ( x, y- декартови координати) и може да бъде в tsіy региона без прекъсвания в ред не по-нисък от първия.

регион гможете да бъдете като неописани, така че бъдете ограничени. как да променя x, yможе да има специфичен биологичен смисъл (концентрация на речи, брой видове) ге положителен квадрант на дясната вертикална равнина:

0 £ х< ¥ ,0 £ г< ¥ .

Концентрацията на речите или броят на забележителностите също може да бъде заобиколен от звяра по обема на съда или от площта на жилищната площ. Тогава площта на стойността на промяната може да изглежда:

0 £ х< x 0 , 0 £ г< y 0 .

промяна x, yв часа те се променят по подобен начин на системата от равни (4.1), така че кожата се превръща в система от две стойности на промените ( x, y).

Гръб, кожен чифт заместители ( x, y) Vіdpovіdaє певчески лагер на системата.

Нека разгледаме областта с координатните оси, върху която x, y. точка на кожата М tsіy ploschіnі vіdpovidає до певческия лагер на системата. Такава равнина се нарича фазова равнина и представлява съвкупността от всички етапи на системата. Точката M (x, y) се нарича изображение или представлява точка.

Нека бъде в часа на часа t = t 0 точки за показване на координати М 0 (х(т 0),y(т 0)). Кожата има момент от време тпоказването на точката ще се промени съответно, за да промени стойността на промяната х(т),y(т). брачна точка М(х(т), Y (т)) На фазовата равнина позицията на всички промени в станциите на системата в процеса на промяна в часа на промяна x(t), y(t) vydpovіdno до rivnyan (4.1), наречен фазова траектория.

Последователността от фазови траектории с различни кочани стойности на промяна дава леснодостъпен "портрет" на системата. побудова фазов портретви позволява да поникнете visnovki за естеството на промяната на промяната x, yбез да познават аналитичните решения на зрителната система(4.1).

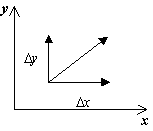
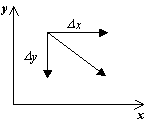
За изображението на фазовия портрет е необходимо да се индуцира векторното поле директно в траекториите на системата в скин точката на фазовата равнина. темпове на растежд t > 0,otrimaemo vіdpovіdnі zbіlshennya д хі д гс viraziv:

д x=P(x, y)д т,

д y = Q(x, y)д т.

офроуд вектор dy/dxв точки ( x, y) Депозит като знак за функция P(x, y), Q(x, y)мога да бъда определен от таблицата:

P (x, y) > 0, Q (x, y) > 0
P(x, y)<0,Q(x,y)<0
P(x, y) > 0, Q(x, y)<0
P(x, y)<0,Q(x,y)>0

.(4.2)

Решението на което y=y(x, c), но по имплицитен начин Ф(x, y)= C,де з- след интегриране, дава семейство от интегрални криви на подравняване (4.2) - фазови траекториисистема (4.1) на равнината x, y.

изоклинен метод

За да предизвикате отлепване на фазовия портрет изоклинен метод -начертайте линии на фазовата равнина, т.е. за преоформяне на интегралните криви под един sing kutom. Уравнението на изоклините лесно се взема от (4.2). годни

де А– много постоянна стойност. смисъл Ае тангенсът на разреза до степента на точката към фазовата траектория и може да приеме стойността на -¥ до + ¥ . представляващ зам dy/dxв (4.2) количеството Авземаме равен изоклин:

.(4.3)

Подравняването (4.3) в основната точка на равнината е равно на една точка до подобна интегрална крива зад винетната точка, de P(x, y)= 0, Q (x, y) = 0 , По начин, който е директно дотистичен, той е невидим, на това, с което става невидимо, значението е подобно:

.

Tsya dot е пунктирана линия на всички изоклини - специална точка.Те се превръщат в нула за една нощ след часа на смяната хі г.

По този начин в специална точка на промяна скоростта на промяна е равна на нула. Също така, особено точката на диференциално подравняване на фазовите траектории (4.2) стационарна система(4.1), а нейните координати са същността на стационарните стойности на променящите се x, y.

От особен интерес за представляване основни изолинии:

dy / dx = 0, P(x, y)=0 – изоклини на хоризонтални dotichnyh i

dy/dx=¥ , Q(x, y)=0 – изоклини на вертикална точка.

Вдъхновявайки заглавия и знаейки смисъла на тяхната греда (X, y), Координати, които удовлетворяват умовете:

ние самите знаем точката на пресичане на всички изоклини на фазовата равнина; ce - точка, Yaka vіdpovіdaє стационарна система(Фигура 4.2).

Системата (4.1) се поддържа от стационарни мелници и има няколко точки на преход на изоклините на главата във фазовата равнина.

Траекторията на скин фазата е показателна за сложността на динамичната система, която преминава през едно и също време, а един ден само един кочан на час.

Ако мислите за теоремите на Коши виконани, тогава през кожата точка на пространството x, y, tпреминават през една интегрална крива. Същото е вярно, завдяки автономия, за фазови траектории: една фазова траектория минава през скин точката на фазовата равнина.

Стабилност на стационарно състояние

Нека системата perebuvaє в гарата rivnovagi.

Същата точка представлява точка, разположена в една от специалните точки на системата, в която са назначени:

.

Stіyka chi не е специална точка, се откроява тим, където chi ni изобразява точка с малък дъх в стационарния лагер. Стосовно към системата от две равни марки на съпротива в движениед, дизглежда като приближаващ се ранг.

Лагерът е ревнив st_yko, сякаш за дадена област, ще бъда издръжлив в бъдеще ще стана ревнив (д )можете да посочите района д (д ), Navkolyshne лагер rivnovagi и volodіє tim vlastіvіstyu, scho odna traektorіya, yak otpjaetsya в средата на областта д , Няма начин да достигнете между д . (Фигура 4.4)

За страхотен клас системи - груби системи – естеството на поведението на тези не се променя с малка промяна в типа на връстниците, информацията за типа поведение в покрайнините на стационарния лагер може да бъде отнета, не напускайте, но да бъдете простени линеаризиранисистема.

Линейни системи.

Нека разгледаме системата от две линейни линии:

.(4.4)

тук а, б, в, г- константи, x, y- Декартови координати във фазовата равнина.

Ще имаме по-сериозно решение при вида:

.(4.5)

Заменете израза в (4.4) и бързо д л т:

(4.6)

Алгебрична система от равенства (4.6) с неизвестно А, Бв този случай има решение по-малко от нула, сякаш е означаващо, сгъване с коефициенти за неизвестно, повече нула:

.

Rozkrivayuchi tsey vyznachnik, otrimaemo характерно изравняване на системата:

.(4.7)

Решението кой е равен получава стойността на шоутол 1,2 , При всякакви възможни ненулеви условия за Аі Бразтвор равен (4.6). Значението на Ци е същността

.(4.8)

Така че вкоренения вираз е отрицателенл 1,2 сложна връзка на числата. Приемливо е обидата на равен корен (4.7) да се разглежда като нула на правилната част и че няма множество корени. Същото глобално решение на системата (4.4) може да бъде представено чрез линейна комбинация от експонента и осцилаторил 1 , л 2 :

(4.9)

За да се анализира естеството на възможните траектории на системата във фазовата равнина е възможно линейна равномерна трансформация на координати, yak позволяват да се изведе системата до канонична форма:

,(4.10)

позволява по-голямо ръчно представяне на фазовата равнина в двойка с изходната система (4.4). Нека представим нови координатиξ , η зад формулите:

(4.1)

От курса на линейната алгебра става ясно, че при различни неравности до нула реални частил 1 , л 2 системата (4.4) след допълнителна трансформация (4.11) винаги може да се трансформира до каноничния вид (4.10) и да промени поведението във фазовата равнинаξ , η . Нека да разгледаме различните vipadki, yakі може да бъде тук.

корен λ 1 , λ 2 - десетичен знак от един знак

В тази посока коефициентите на трансформация на действието преминаваме в зоната на действиеx, yдо делящата се равнина ξ, η. След като разделите приятел на равни (4.10) на костур, той се взема:

.(4.12)

Интегриращата цел, знаем:

де (4.13)

Домашна интелигентност pіd λ 2 коренът на характерното изравняване с великия модул, който не разрушава кохерентността на нашата световност. Todі, oskіlki в този тип корен λ 1 , λ2 - изчисти един знак,а>1 , не мога да използвам интегрални криви от параболичен тип вдясно.

Всички интегрални криви (оси на крим η , Yakіy vіdpovіdaє ) Stosuyutsya на кочана на осовите координати ξ, както и интегралната крива на подравняване (4.11). Кочанът на координатите е единична точка.

Z'yasuєmo сега директно ruhіv си представя точки vzdovzh фазови траектории. така че λ 1, λ2 - отрицателен, тогава, както се вижда от равни (4.10), | ξ |, | η | промяна във времето. Изобразяващата точка се приближава до кочана на координатите, но не го достига. По друг начин беше изключително очевидно, че теоремата на Коши ще докаже, че само една фазова траектория минава през скин точката на фазовата равнина.

Такава специална точка, през яка, за да премине интегралните криви, подобно на преди, като семейство параболи преминават през кочана на координатите, носят името на възела (фиг. 4.5)

Мелницата е равна на типа вузол при λ 1, λ2 < 0 стабилно според Ляпунов, така че точката на цялата интегрална крива се свива право напред до кочана на координатите. tse стабилен вузол. Yakscho w λ 1, λ2 > 0, тогава | Ξ |, | η | расте в разумен час и показва точката, която се движи напред, в кочана от координати. Има специална точка, в която vipadka– нестабилен вузол .

На фазовата равнина x, y глобалният yakіsny характер на поведението на интегралните криви се запазва, аледотичните спрямо интегралните криви не се вписват в координатните оси. Kut nakhil tsikh dotichnyh bude vyznachatsya spіvvіdnoshnannya koefіtsіentsіv α , β , γ , δ в равни (4.11).

корен λ 1 , λ 2 - описателни и различни знаци.

трансформация вкоординати x, y до координати ξ, η пак знам. Rіvnyannia за canonіchnyh zmіnnih отново може да изглежда (4.10), но сега знаците λ 1, λ2 различно. Може да се види подравняването на фазовите траектории:

де, (4.14)

Интегрирайки (4.14), знаем

(4.15)

tse подравняването дефинира семейство от криви от хиперболичен тип, отклоняващи се координатните оси- асимптоти (при а=1 mi mali b семейство равнобедрени хиперболи). Координатните оси і в правилната посока са интегрални криви– ще има единични интегрални криви, които преминават през кочана от координати. кожате добавят до три фазови траектории: от две ruhіv да ревнувам (иначе ще ревнувам) и от ревнувам. Всички други интегрални криви– същността на хиперболата, която не минава през кочана от координати (фиг. 4.6) Такава специална точка се нарича "сидло ». Линиите на реката в близост до планинската седловина се водят като фазови траектории в покрайнините на седловината.

Нека разгледаме естеството на движението, изобразявайки точките по фазовите траектории близо до станцията на равните. хайде напримерλ 1 > 0, λ 2<0 . Тоди изобразява точка, поставена върху оста ξ , Ще бъде преместен от кочана на координатите, но ще бъде поставен върху оста η – ще бъде възможно да се доближите до кочана на координатите, не достига до йога през последния час. De b не знаеше смисъла в момента на кочана η =0), няма да е в края на рахунка, ще отида по-далеч, ще стана ревнив, ще го навия на кочан, ще се срути по една от интегралните криви право напред до специална точка.

Очевидно какво специална точка към вида на седалката . Само със специално проектирани кочани умове на асимптотитеη =0 системата ще се приближава, докато не започна да ревнувам. Въпреки това, не пренебрегвайте твърденията за несъвместимостта на системата. как да уважаваме, ако всички кочани ще станат системи във фазовата равнина на различни пътища, тогава неподвижността на такъв кочан ще стане, сякаш е директнапреди специални точки, водещи до нула. За това, независимо дали е истинско или не, ще видите системата и ще станете ревниви.Връщам се обратно към координатитеx, yотнемаме същата картина на естеството на движението на траекториите върху кочана на координатите.

Близо до кордона между погледнатите вапки на възела и седлото е изпадък,ако едно от характерните индикации, напр λ 1 , изчезва до нула, какво е мястото, ако системата е лидер- вираз ad-bc = 0(Див. Формула 4.8 ). В този случай коефициентите на десните части са равни (4.4) пропорционални на едно към едно:

и системата може да изравни всички точки от правата със своите лагери:

Мрежата от интегрални криви е семейство от успоредни прави линии с коефициент на върха , Зад които точките или се приближават, за да станат равни, или се отдалечават от новата по угар като знак за друг корен от характерното изравняване λ 2 = а + г.(фиг.4. 7 ) От тази гледна точка координатите ще станат равни на стойността на кочана на промяната.

корен λ 1 , λ 2 – комплексpo'yazanі

В същото настроение с течениетохі гние ще майки на сложни пов'язани ξ , η (4.10) . Въпреки това, като се въведе още една междинна трансформация, може по същия начин да се търси десетична линейна равномерна трансформация. годни:

(4.16)

де а, б,і u, v – ефективни стойности. Можете ли да покажете, че трансформацията еx, yпреди u, v є с нашите надбавки, ние сме описателни, линейни, хомогенни с детерминантата, водеща нула. По силата на равен(4.10, 4.16) може би:

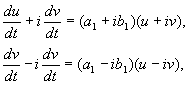
звезди

(4.17)

Като раздели приятел с равни на костур, Ние взимаме:

по-лесно е за интегриране, Как да преминете към полярна координатна система (г, φ ) . след замяна otrimaemo, zvіdki:

.(4.18)

В този ред, на фазовата равнинаu, vможем да правим със семейство от логаритмични спирали, кожата можеасимптотична точка на кочана на координатите.Точката е специална, тъй като е асимптотична точка на всички интегрални криви, които могат да изглеждат като спирали, инвестирайки един вприятел, обади се фокус ( фиг.4.8 ) .

Нека разгледаме естеството на руху изображението на точките по фазовите траектории. Умножаване на първото е равно (4.17) поu, и един приятел на vи като добавим, вземаме:

де

Хайде а 1 < 0 (а 1 = Reλ ) . Изображението на една и съща точка непрекъснато се приближава до кочана на координатите, като не го достига в последния час. Tse означава, че фазовите траектории са усукващи спирали и причиняват избледняващ colivingпромяна. ce - постоянен фокус .

При друг стабилен фокус, като различен бърз възел, не само умът на Ляпунов се пееше, но все по-често. Сама по себе си, в случай на вентилация на кочана, системата ще се обърне за един час, както винаги близо до равното положение. Такава издръжливост, с такъв кочан дъх, не само не расте, но избледнява, нараства до нула, вика абсолютна непоколебимост .

Каква е формулата (4.18) а 1 >0 , Тогава точката се показва като кочан от координати и може да сме отдясно нестабилен фокус . При пресичане на самолетаu, vкъм фазовата равнинах, гспиралите също са покрити със спирали, протекторът ще се деформира.

Нека сега да разгледаме випадка, акоа 1 =0 . Фазови траектории на самолетаu, vще има кръгове Яким на апартаментаx, yvіdpovіdat elіpsi:

По такъв начин приа 1=0 през специална точкаx= 0, Y = 0 не преминават през една и съща интегрална крива. Такава единична точка е изолирана, близо до която интегралните криви са затворени криви, зокреми, елипси, едно към едно вноски и задушават единична точка, наречена център.

По този начин шест типа могат да се изравнят в угар поради естеството на корените на характеристиката равен (4.7). Изглед на фазовите траектории в равнината x, yза тези шест изгледа на изображенията на фиг. 4.9.

Мал 4.9.Видове фазови портрети в близост до стационарен лагер за система от линейни подравнявания (4.4).

Пет вида ще станат еднакви груби, характерът им не се променя с малки промени в десните части на равния (4.4). При някаква дребна вина, но сменете не само правилните части, а първата поръчка. Шосте стан ривноваги - център - груб. При малки промени в параметрите от дясната страна, равните части на вината преминават в стабилен или нестабилен фокус.

бифуркационна диаграма

Нека въведем обозначението:

. (4.11)

По-характерно е да запишете при гледката:

. (4.12)

Нека разгледаме равнината с правоъгълни декартови координати с , д и е значимо в този регион, тъй като изглежда показва, че ще стана ревнив от друг тип, който се отличава с естеството на корените на характерната ревност

.(4.13)

Ще стана интелектуално непоколебимо ревниво за проявата на негативната част от действиетол 1 и л 2 . Необходим и достатъчен ум tsgogo - vikonannya nerіvnostiс > 0, д > 0 . На диаграмата (4.15) tsіy umovі vіdpovіdat точки, roztashovanі в първата четвърт на равнината parametrіv. Специален момент ще бъде фокусът, катол 1 и л 2 комплекс. Tsіy ум vіdpovіdat tі точки на равнината, за тези , tobto точки между два клона на параболас 2 = 4 д. точки pivvіs с = 0, д> 0, направете мелниците равни на централния тип. по същия начин,л 1 и л 2 - dіysnі, але различни знаци, така че специална точка ще бъде седло, като д<0, и т.н. В подторбата вземаме диаграмата на разпределението на площта на параметрите с, д, В региона, yakі vіdpovіdat vyznym видове ще стана ревнив.

Мал 4.10.бифуркационна диаграма

за системата от линейни линии 4.4

Какви са коефициентите на линейната система а, б, в, глежат под текущия параметър, тогава при промяна на параметъра стойностите ще се променятс , д . При преминаване през кордоните характерът на фазовия портрет се променя доста ясно. Ето защо кордоните се наричат ​​бифуркации – според различните страни на кордона системата има два топологично различни фазови портрета и, очевидно, два различни типа поведение.

Диаграмата показва как могат да бъдат направени такива промени. Ако включите специално випадите - кочана на координатите, тогава е лесно да бачите, че седалката може да влезе във вузол, стабилен или нестабилен при промяна на оста на ординатите. Стабилен вузол може да отиде или до седло, или до стабилен фокус и т.н. Важно е, че преходът на стабилен вузол - стабилен фокус и нестабилен вузол - нестабилен фокус не са бифуркации, тъй като топологията на фазовото пространство не се променя с това. Ще говорим по-подробно за топологията на фазовото пространство и бифуркационните преходи в Лекция 6.

По време на бифуркационните преходи се променя естеството на стабилността на определена точка. Например, стабилен фокус през центъра може да се превърне в нестабилен фокус. Тази бифуркация се нарича Бифуркация Андронов-Хопфпо имена те продължиха її вчених. С тази бифуркация в нелинейни системи се ражда граничен цикъл и системата става самоосцилираща (раздел. Лекция 8).

дупето. Система от линейни химични реакции

реч х prikaє zzovnі z постоянно swidkistyu, трансформиране в реч Y і zі swidkistyu, пропорционална концентрация на речта Й, Погледнато от обхвата на реакцията. Всички реакции са от първи ред, след малко вино ще добавя речта на призива, има нулев ред. Схемата на реакцията може да се види:

(4.14)

и да бъде описана от системата за равенство:

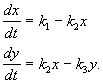(4.15)

Стационарните концентрации се отнемат, приравнявайки правилните части на нула:

.(4.16)

Нека да разгледаме фазовия портрет на системата. Нека разделим още едно изравняване на системата (4.16) на персийски. предприеме:

.(4.17)

Уравнение (4.17) означава поведението на променливите във фазовата равнина. Нека имаме фазов портрет на цялата система. На задната част на главата има няколко субклинични линии във фазовата равнина. Подравняване на изолиниите на вертикалните докове:

Rivnyannya іzoklini хоризонтални dotichnyh:

Специална точка (стационарен лагер) лежи върху перетината на изоклините на главата.

Сега е важно, под някакъв разрез, координатните оси на интегралните криви са оцветени.

yakscho x= 0 тогава.

В този ранг тангенсът на кутата е безумно дотичен спрямо интегралната крива y=y(x),преоформете всички ординати х=0, Отрицателно на горната повърхност (познайте какво се променя x, y mayyut стойности на концентрацията и към това имаме само десния горен квадрант на фазовата равнина). При това стойността на тангенса на кута нахил дотично нараства с разстояние от кочана на координатите.

Нека разгледаме всичко y= 0. В случай на кръстовище, tsієї osі, вонята се описва с интегралните криви

в тангенсът на разреза в движение на интегралните криви, така че да се промени цялата абциса, положителна и да се увеличи от нула до безкрайност или да се увеличи х.

В.

След това, с леко увеличаване на тангенса на кутата, той смело се променя след абсолютната стойност, оставяйки отрицателната стойност до -1 при х ® ¥ . Познавайки директно dotichnyh до интегрални криви на изолиниите на главата и на координатните оси, е лесно да се предизвика цялата картина на фазовите траектории.

Естеството на съпротивлението на дадена точка може да се установи с помощта на метода на кората на Ляпунов. Характерният знак на системата може да изглежда така:

.

Razkrivayuchi vyznachnik, otrimaemo характеристика на изравняване на системата: , Тобто корените на характерната ревност на негодуванието са отрицателни. По-късно стационарният лагер на системата е стабилен вузол. При каква концентрация на речта х Pragne до стационарно състояние винаги е монотонно, концентрацията на речта Y може да премине през min или max. Режимите на бобината в такава система не са възможни.

Основно разбиране и цел:

Нулата на аналитичната функция f (z) е точката "a", за която f (a) = 0.

Нулата до порядъка "n" на функцията f (z) е точката "a", точно както fn (a) ¹0.

Особена точка "a" се нарича изолирана особена точка на функцията f (z), тъй като е близо до центъра на точката, в която няма особени точки, крем "a".

Има три вида изолационни точки:.

1 изброяване на специални точки;

3 точно единични точки.

Видът на сингулярната точка може да се определи от поведението на дадена функция в намерената особена точка, както и от формата на реда на Лоран, взет за функцията в близост до намерената особена точка.

Присвоява се на типа на специална точка от поведението на функцията в нея.

1. Премахване на специални точки.

Изолирана особена точка a на функцията f (z) се нарича изолирана точка, която е главната граница.

2. Поляци.

Изолирана особена точка a на функцията f (z) се нарича полюс, т.е .

3. Източна сингулярност на точка.

Изолирана особена точка a на функцията f (z) се нарича присъщо сингулярна точка, тъй като няма завършвания или несъответствия.

Между нулите и полюсите на функцията има връзка.

За да бъде точката a полюс от порядък n на функцията f (Z), е необходимо и достатъчно точката да бъде нула от порядък n за функцията.

Ако n = 1 полюс се нарича прост.

среща:Изолирана точка с уникален характер се нарича:

а) хлътнал, като главната част на оформлението на деня;

б) прът, който е главната част за отмъщение за последния брой членове;

в) само специална точка, сякаш основната част е да отмъсти на неизчерпаем брой членове.

а) В такъв ранг, в близост до неизползвания специален пункт за разполагане, мога да видя:

vono vyslovlyuє функция във всички точки на залога | z-a |

В центъра z = a равенството не е правилно, тъй като функцията при z = a може да бъде разширена, а дясната част е непрекъсната. Ако промените значението на функцията в центъра, като я вземете равно на значението на дясната част, след като я откриете, звездите и името ще бъдат елиминирани.

б) В близост до полюса, в порядъка на m, може да се види подредбата в реда на Лоран:

в) В близост до обикновен стълб

Ревизия и формули за тяхното изчисляване.

Вариацията на аналитичната функция f (z) в изолираната сингулярна точка z 0 се нарича комплексно число, което е равно на стойността на интеграла , взета в положителна посока по протежение на залога L с център в точката z 0, която се намира в областта на аналитичност на функцията f (z) (т.е. в окръжността 0<|z-z0|

Функцията f (z) в изолираната особена точка z 0 се обозначава със символа Res f (z 0) или Res (f (z); z 0). по такъв начин,

Resf (z 0) = . (22.15.1)

Ако поставим n = -1 във формула (22.15.1), тогава вземаме:

C1 =

или Res f (z 0) = C -1,

За да се извлече функцията f (z), така че сингулярната точка z 0 да е равна на коефициента при първия член с отрицателен показател в разлагането на функцията f (z) в ред на Лоран.

Изчисляване на обезщетението.

Правилно изброяване на единични точки. Очевидно, ако z \u003d z 0 е правилен или сингулярната точка на функцията f (z) е изчерпателна, тогава Res f (z 0) = 0 (в разширението на Лоран в тези случаи частта на главата е същата, така че c-1 \u003d 0).

полюс. Нека точката z 0 е полюсът на функцията f (z). Тогава редът на Лоран за функцията f (z) около точката z 0 може да изглежда така:

Zvіdsi

За това, преминавайки в tsіy равновесие към границата при z -z 0, е необходимо

Res f (z0) =

Істотно специална точка. Ако точката z 0 е абсолютно особена точка на функцията f (z), тогава за да изчислите грешката на функцията в тата точка, използвайте коефициента c-1 в разширението на функцията в редицата на Лоран.

Класификация на подразделения. Сума, твир под, тяхната сила, графично представяне.

Следвайте, за да споделите на:

1. Випадкови

2. Надежден

3. Невъзможно

Dostovirne - tse такава подия, сякаш е obov'yazkovo в тези умове (за нощта след раните).

Випадкове - това е под_я, як можеш да се събудиш, а може би няма да се събудиш (задача за сън).

Невъзможно - tse такъв podіya, як в тези умове не идва (има достатъчно зелени маслини от кутията само с chervonim).