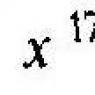Momentu transformācija inercē ar paralēlu asu pārnesi. Mainot inerces momentus, kad koordinātu asis tiek pārvietotas paralēli. Statiskie momenti Piešķirti svarīguma centram

Asis, kas iet caur plakanas figūras smaguma centru, sauc par centrālajām asīm.
Inerces momentu parasti sauc par centrālo inerces momentu.

Teorēma

Inerces momentam jābūt vienādam ar inerces momenta summas asi, ja centrālā ass ir paralēla dotajai, tas ir, lai pievienotu figūras laukumu kvadrātam starp asīm.

Lai pierādītu teorēmu, apskatīsim diezgan plakanu figūru, kuras laukums ir lielāks A , centrs W , un centrālais inerces moments ir ap asi x gribu Es x .
Aprēķināsim figūras inerces momentu pēc darbības ass x 1 , paralēli centrālajai asij un attālumā tajā uz statīva a (Mal).

I x1 = Σ y 1 2 dA + Σ (y + a) 2 dA =
= Σ y 2 dA + 2a Σ y dA + a 2 Σ dA.

Analizējot otrimana formulu, ir svarīgi, lai pirmais papildinājums būtu aksiālais inerces moments pa centrālo asi, otrs papildinājums ir figūras kvadrāta statiskais moments pa centrālo asi (pazīstams arī kā nulle), bet trešais. papildinājums, kurā aplūkota reprezentāciju integrācija a 2 A , kā rezultātā mēs ņemam formulu:

I x1 \u003d I x + a 2 A- Teorēma ir pabeigta.

Pamatojoties uz teorēmu, ir iespējams izgatavot visnovok, kas rindā paralēlās asis plakanas figūras aksiālais inerces moments būs mazākā centrālās ass vērtība .

Galvas asis un galvas inerces momenti

Izveidosim plaknes figūru, inerces momenti kā koordinātu asis Es x і Es y , un polārais inerces moments ir līdzīgs koordinātu vālītei Es ρ . Kā tas tika instalēts agrāk,

I x + I y = I ρ.

Ja koordinātu asis griežas savā plaknē uz koordinātu vālītes, tad polārais inerces moments paliks nemainīgs, un momenta asis mainīsies, to daudzums tiks zaudēts par konstantes lielumu. Mainīgo vērtību summas šķembas ir nemainīgas, viena no tām mainās, bet otra palielinās, un navpaki.
Arī asu pirmajai pozīcijai viens no aksiālajiem momentiem sasniedz maksimālo vērtību, bet otrs - minimālo.

Osі, shdo tādi inerces momenti var būt minimāli maksimālā vērtība sauc par galvas inerces asīm.
Inerces momentu, tāpat kā galvas asi, sauc par galvas inerces momentu.

Ja galvai ir jāiet cauri figūras galvas centram, to sauc par galvas centrālo līniju, un inerces moments, piemēram, šī ass, ir galvenais centrālais inerces moments.
Jūs varat veikt visnovok, lai skaitlis būtu simetrisks kā ass, tad visi būs viena no galvas centrālajām figūras inerces asīm.

Centrālais inerces moments

Plakanas figūras centrālo inerces momentu sauc par visu elementāru maidančiku radījumu summas laukumu līdz divām savstarpēji perpendikulārām asīm:

I xy = Σ xy dA,

de x , y - Vіdstan vіd maidanchik dA uz cirvjiem x і y .
Centrālais inerces moments var būt pozitīvs, negatīvs un vienāds ar nulli.

Centrālais inerces moments ir iekļauts asimetrisko pārtēriņu galveno asu stāvokļa noteikšanas formulā.
Standarta profilu tabulām ir raksturlielums, ko sauc inerces rādiuss , ko aprēķina formulām:

i x = √ (I x / A),i y = √ (I y / A) , (Šeit es devu zīmi"√"- saknes zīme)

de Es x, es y - ass inerces momenti pererazu pa centrālajām asīm; A - Šķērsošanas zona.
Tsya ģeometriski raksturīga vikoristovuetsya pozacentral stiepjas chi saspiežot, un navit vēlu wigina.

Vērpes deformācija

Pamata izpratne par vērpšanu. Pagriežams apaļš stars.

Par vērpšanu sauc šo deformācijas veidu, kad sijas šķērsgriezumā ir tikai neliels moments, lai sagrieztos, tad tas ir spēka faktors, kas izraisa apļveida nobīdi pa asi, perpendikulāri asij, vai pāreju uz tāda nobīde. Citiem vārdiem sakot - tiek vainotas vērpes deformācijas, lai līdz taisnam stieņam plaknēs, kas ir perpendikulāras šai asij, tiek pielikts pāris vai pāris spēku.
Šo spēku pāru momentus sauc par vērpšanu vai ietīšanu. Obertāls brīdis nozīmē T .
Tādā veidā garīgi podіlyaє spēka faktori un deformācijas vērpjot uz zvnіshnі (griešanās, stāvi momenti). T ) un iekšējie (vērpes momenti M kr ).

Vīšanas mašīnās un mehānismos visbiežāk izmanto apaļas vai cauruļveida vārpstas, tāpēc šādiem mezgliem un detaļām visbiežāk izmanto rozrahunki maigumam un cietībai.

Apskatīsim apaļas cilindriskas vārpstas vērpšanu.
Lai atklātu humusa cilindrisku vārpstu, kaut kādos ātros stiprinājumos viens no galiem, un virspusē ir aizmugurējo līniju un šķērsenisko ķīļu režģis. Vārpstas brīvajam galam, perpendikulāri vārpstas asij, tiek pielikti pāris spēki, lai ass būtu savīti. Ja uzmanīgi aplūkojat acs līnijas uz vārpstas virsmas, varat atzīmēt, ka:
- visa vārpsta, kā viņi sauc par vispusīgo pagriezienu, atbrīvojas no taisnās līnijas;
- kіl diametram jābūt vienādam, un atšķirība starp susіdnіmi likmēm nemainīsies;
- Vēlāk līnijas uz vārpstas pārvēršas dvīņu līnijās.

Tāpēc ir iespējams izgatavot visnovok, ka, sagriežot apaļu cilindrisku stieni (vārpstu), hipotēze par plakaniem pārgriezumiem ir spēkā, kā arī pieļauj, ka kilu rādiusi deformējoties kļūst taisni (to diametra ķemmīšgliemenes nav izmaiņas). Šķembas ikdienas vēlu spēku šahtās, tad rūpējieties par tām.

Iedegums, deformatsia krutnya Apaļa vārpsta PoleAєє pagriezienā šķērsvirziena pasažierim, viens vienīgs Navko Osi Kratchennya, brieching Kutov Vіd Vіdkypleniy Perezіza - Chim Dali Vіd Skrіplain Kіntza Valo Valeki-Skump Vādkumps Perezsi Kutz,
Lai veiktu vārpstas ādas griezumu, pagrieziet vārpstas daļas vērpšanu, kas atrodas starp griezumiem un rīklēm (nostiprina ar griezumu).


Kut ( Mal. viens) vārpstas brīvā gala (griezuma gala) pagriešana tiek saukta par cilindriskās sijas (vārpstas) vērpšanas augšējo galu.
Vіdnosny kutom vērpjot φ 0 sauc par tinumu kuta vērpšanu φ 1 uz vіdstan l 1 no pirmā griezuma līdz hipotēkai (fiksēts griezums).
Yakshcho cilindrisks kokmateriāls (vārpsta) zavdovka l ja uz brīvā gala (kas veidojas no viendabīga ģeometriska gabala) notiek pastāvīga pārgriešana un griešana ar vērpšanas momentu, tad ir taisnība:
φ 0 = φ 1 / l 1 = φ / l = konst - Pastāvīga vērtība.

Kā atpazīstami tieva bumbiņa uz viscerāla humusa cilindriska stara virsmas ( Mal. viens), apkārtne režģa vidū cdef , tad ir cieņā, ka šis centrs deformācijas laikā deformēsies, un її puse, kas atrodas tālu no fiksētā griezuma, tiek nobīdīta sijas pagrieziena pusē, ieņemot pozīciju cde 1 f 1 .

Jāņem vērā, ka šuves deformācijas laikā vērojama līdzīga aina, tikai vienā virzienā virsma tiek deformēta translācijas kustībā vienā virzienā, nevis aptīšanas kustībā, kā vērpjot deformācijas gadījumā. Uz šī balsta var pievienot viņnovus, kuri, griežoties šķērseniskajos griezumos, vaino tikai punktveida iekšējos spēkus (spriegojumu), kas fiksē momentu, kuru griezt.

Arī vērpšanas brīdis ir iekšējo dotichnyh spēku, kas attīstās šķērsgriezumā, staru ass rezultējošais moments.

2. Platības statiskie momenti pāri asu platumam Ozі Oy(div 3, m 3):

4. Centrālais inerces moments visā asu platumā Ozі Ak!(Skatīt 4, m 4):

Tad Oscilki

Ass Jzі Jy ka polārais Dž p inerces momenti vienmēr ir pozitīvi, lauskas zem integrāļa zīmes ir citas pasaules koordinātes. Statiski mirkļi Szі Sy, kā arī centrālais inerces moments Jzy var būt gan pozitīva, gan negatīva.

Ruļļu tērauda velmēšanas diapazonā ir norādītas centra momentu vērtības aiz moduļa. Rozrahunkām ir šādas nozīmes iegūšanai zīmes uzlabošanai.

Spoles centra momenta zīmes apzīmēšanai (3.2. att.) ir pamanāms, ka ir redzama trīs integrāļu summa, jo tie tiek aprēķināti tikai tām perifērijas daļām, kuras ir izkliedētas ceturtdaļās. koordinātu sistēma. Ir skaidrs, ka daļām, kas izplatās 1. un 3. ceturksnī, mums būs pozitīva integrāļa vērtība, zydA būs pozitīvi, un integrāļi, kas tiek aprēķināti daļām, izkliedējot II un IV ceturksnī, būs negatīvi (tvir zydA būt negatīvam). Otzhe, par kutochka attēlā. 3.2, un centrālā inerces momenta vērtība būs negatīva.

Rozmirkovuyuchi līdzīgs rangs pārgriešanai, lai, ja jūs vēlaties vienu veselu simetriju (3.2. att., b), jūs varat izgatavot visnovku, tāpēc centrālais inerces moments J zy ir vienāds ar nulli, jo viena no asīm (Oz vai Oy) ir pilnīgi simetriska griezumam. Noteikti, ka daļām trikotāžas, roztashovannyh ūdens centra 1. un 2. ceturksnī, inerces moments tiek ņemts vērā tikai kā zīme. Var teikt, ka ir vairākas daļas, kas atrodamas III un IV ceturksnī.

Statiskie momenti Piešķirti svarīguma centram

Aprēķināmi statiskie momenti plašam asu klāstam Ozі Oy attēlā parādītais taisnstūris. 3.3.

Rīsi. 3.3. Līdz statisko momentu aprēķinam

Šeit: A- šķērsošanas zona, yCі z C- Smaguma centra koordinātas. Taisnstūra smaguma centrs tiek mainīts uz diagonālēm.

Acīmredzot, ja asis, kurās tiek aprēķināti statiskie momenti, iet caur figūras smaguma centru, tad tās koordinātas sasniegs nulli ( z C = 0, yC= 0), i, līdzīgi kā formula (3.6), statiskie momenti un vienādi ar nulli. tādā veidā, krosovera smaguma centrs ir punkts, kuram var būt šāda jauda: statiskais moments, lai kāda būtu ass, lai tam izietu cauri.,nulle.

Formulas (3.6) ļauj uzzināt smaguma centra koordinātas z Cі yC saliekamās formas šķērsgriezums. Jakščo peretinu var dot pie redzesloka n daļām, kas atrodas mājas zonā un smaguma centrā, tad visa šķērsgriezuma smaguma centra koordinātu aprēķinu var uzrakstīt šādi:

.

(3.7)

Inerces momentu maiņa ar paralēlu asu pārnesi

Ļaujiet man redzēt inerces momentus Jz, Jyі Jzy shodo cirvji Oyz. Ir nepieciešams aprēķināt inerces momentu Dž.Z, Dž. Jі JZY shodo cirvji O 1 YZ, paralēli asīm Oyz(3.4. att.) a(horizontāli) un b(vertikāli)

Rīsi. 3.4. Inerces momentu maiņa ar paralēlu asu pārnesi

Elementārā maidančika koordinātes dA saistīt sevi ar šādām līdzvērtībām: Z = z + a; Y = y + b.

Aprēķināsim inerces momentus Dž.Z, Dž. Jі JZY.

(3.8)

(3.9)

(3.10)

Kāds punkts O cirvji Oyz skrien ar punktu W- pereses smaguma centrs (3.5. att.); statiski momenti Szі Sy kļūst vienādi ar nulli, un formulas saka Y i Zi Ir jāņem ar simbolu uzlabošanu. Uz inerces momenta ass nevar ievietot koordinātu zīmes (koordinātes tiek pārvietotas uz citu soli), bet uz centrālā inerces momenta koordinātu zīme rindā (izveide Z i Y i A i var būt negatīvs).

Bieži vien praktisko uzdevumu gadījumā ir nepieciešams apzīmēt inerces momentus pāri asīm, dažādās orientācijās vienā plaknē. Ja jums ir manuāli jāpielāgo momenta vērtība visa krosovera inercē (pirms visām noliktavas daļām), ir arī citas asis, kuras var atrast tehniskajā literatūrā, īpašos rādītājos un tabulās, kā arī pieskatīt formulas. Tāpēc ir svarīgi izveidot papuves starp viena un tā paša dažādu asu krustojuma inerces momentiem.

Savvaļas veidā pāreju no vecās uz jauno koordinātu sistēmu var uzskatīt par divām secīgām vecās koordinātu sistēmas transformācijām:

1) koordinātu asu paralēlās translācijas ceļš jaunajā pozīcijā

2) veids, kā pagriezt їх shodo jaunu koordinātu vālīti. Apskatīsim pirmo no šīm transformācijām, tas ir, koordinātu asu paralēlu pārnešanu.

Pieļaujams, ka veco cirvju thogo šķērsgriezuma inerces momenti (18.5. att.) atrodas mājā.

Ņemsim jaunu koordinātu sistēmu no asis, kas ir paralēlas mums pašiem. Būtiski a un b ir punkta koordinātas (jaunās koordinātu vālītes) vecajā koordinātu sistēmā

Apskatīsim vecās koordinātu sistēmas elementāro apgabalu Koordinātas її y ir vienāds ar y i . Jaunā sistēma smird vienādi

Mēs varam attēlot aksiālā inerces momenta koordinātu vērtību ap asi

Citādi - inerces moments ir krosovera statiskais moments pa krosovera ceļa laukuma F asi.

Oce,

Ja viss z iet caur griezuma smaguma centru, tad statiskais moments i

No formulas (25.5) var redzēt, ka inerces momentam jābūt kā asij, lai tas neizietu cauri smaguma centram, lielākam par inerces momentu asij, kas iet caur smaguma centru, par jūga apjoms ir pozitīvs. No tā paša inerces momenta, kad tas ir paralēls asīm, aksiālais inerces moments ir vismazākais, lai ass izietu caur šķērsgriezuma smaguma centru.

Inerces moments ap asi [pēc analoģijas ar formulu (24.5)]

Okremajā kritienā, ja viss iet caur griezuma smaguma centru

Formulas (25.5) un (27.5) plaši izmanto, aprēķinot locīšanas (noliktavas) pārskrējienu aksiālos inerces momentus.

Tagad mēs varam iedomāties centrālā inerces momenta vērtību asu platumam

Apskatīsim plakanās figūras (att.) inerces momentu asīm $(Z_1)$ un $(Y_1)$ dotajiem inerces momentiem asīm $X$ un $Y$.

$(I_((x_1))) = \int\limits_A (y_1^2dA) = \int\limits_A (((\left((y + a) \right)))^2)dA) = \int\limits_A ( \left(((y^2) + 2ay + (a^2)) \right)dA) = \int\limits_A ((y^2)dA) + 2a\int\limits_A (ydA) + (a^2 )\int\limits_A (dA) = $

$ = (I_x) + 2a(S_x) + (a^2)A$,

de $(S_x)$ - figūras statiskais moments ir ap asi $X$.

Līdzīgi kā asij $(Y_1)$

$(I_((y_1))) = (I_y) + 2a(S_y) + (b^2)A$.

Centrālais inerces moments asīm $(X_1)$ un $(Y_1)$

$(I_((x_1)(y_1))) = \int\limits_A ((x_1)(y_1)dA) = \int\limits_A (\left((x + b) \right)\left((y + a) ) \right)dA) = \int\limits_A (\left((xy + xa + by + ba) \right)dA) = \int\limits_A (xydA) + a\int\limits_A (xdA) + b\int \limits_A(ydA) + ab\int\limits_A(dA) = (I_(xy)) + a(S_x) + b(S_y) + abA$

Visbiežāk notiek pāreja no centrālajām asīm (plakanās figūras augšējās asis) uz pilnajām, paralēlajām. Tad $(S_x) = 0$, $(S_y) = 0$, ass $X$ un $Y$ lauskas ir centrālas. Atlikušais majons

de, - spēka inerces momenti, tas ir, inerces momenti atbilstoši centrālo asu jaudai;

$a$, $b$ - vіdstanі vіd centrālās asis uz analіzovanih;

$A$ - figūras laukums.

Jāņem vērā, ka, piešķirot centrālo inerces momentu lielumiem $a$ un $b$, pie vainas ir zīme, tā ka smirdēšana faktiski ir figūras smaguma centra koordinātes. cirvji, uz kuriem skatās. Piešķirot aksiālos inerces momentus un vērtības, vērtības tiek uzrādītas aiz moduļa (kā standartā), tomēr smakas lauskas paceļas kvadrātā.

Paralēlo pārsūtīšanas formulu palīdzību iespējams mainīt pāreju no centrālajām asīm uz pilnajām, vai no otras puses- prevіlnyh centrālajās asīs Pirmā pāreja ir atzīmēta ar "+" zīmi. Vēl viena pārbrauktuve ir atzīmēta ar zīmi- ".

Pielietojiet dažādas formulas pārejai starp paralēlām asīm

Taisnstūra tīklene

Būtiski taisnstūra centrālais inerces moments ir proporcionāls galvenajiem inerces momentiem ap $Z$ un $Y$ asīm.

$(I_x) = \frac((b(h^3)))(3)$; $(I_y) = \frac((h(b^3)))(3)$.

.

Līdzīgi $(I_y) = \frac((h(b^3)))((12))$.

Trikutny Pereriz

Zīmīgi, ka trijutera centrālais inerces moments pār doto bāzes inerces momentu $(I_x) = \frac((b(h^3)))((12))$.

.

Ja centrālajai asij $(Y_c)$ ir cita konfigurācija, tad varam arī to apskatīt. Visu figūru inerces moments pa asi $(Y_c)$ ir lielāks par trikotāžas $ABD$ inerces momenta pa asi $(Y_c)$ un trikotāžas $CBD$ inerces momenta summu. pa asi $(Y_c)$, tobto

.

Iecelšana uz salocītās sliedes inerces momentu

Saliksim kopā svarīgo peretin, kas sastāv no okremih elementiem, ģeometriskās īpašības kāds zināms. Noliktavas figūras laukums, statiskais moments un inerces moments summējas par noliktavas attiecīgo raksturlielumu summu. Tāpat kā perimetra ieloces, jūs varat padarīt to līdzīgu vienai no figūrām no ārpuses, ir redzamas figūras ģeometriskās īpašības. Piemēram, noliktavas figūras inerces momenti, kas parādīti att. parādīsies šādi

$I_z^() = \frac((120 \cdot ((22)^3)))((12)) - 2 \cdot \frac((50 \cdot ((16)^3)))((12) )) = 72 \, 300 $ cm 4 .

$I_y^() = \frac((22 \cdot ((120)^3)))((12)) - 2 \cdot \left((\frac((16 \cdot ((50)^3)) )((12)) + 50 \cpunkts 16 \cpunkts ((29)^2)) \labais) = 1\.490\.000 $cm 4

Mēs ieviešam Dekarta taisnstūra koordinātu sistēmu Oxy. Apskatīsim dovіlny peretina koordinātu plakni ( slēgta zona) no apgabala A (1. att.).

Statiski mirkļi

Punkts C ar koordinātām (x C, y C)

sauca smaguma centrs.

Ja koordinātu asis iet caur malas smaguma centru, tad malas statiskie momenti sasniegs nulli:

Aksiālie inerces momentišķērsošanu pa x un y asīm sauc par formas integrāļiem:

Polārais inerces moments Koordinātu vālītes krustpunktu sauc par formas integrāli:

Centrālais inerces moments sadaļu sauc par prāta integrāli:

Galvas inerces asis ir nogrieztas sauc divas savstarpēji perpendikulāras asij, kur I xy =0. Attiecībā uz savstarpēji perpendikulārajām asīm є visa griezuma simetrija, tad I xy \u003d 0 i, arī qi ass - smuki. Tiek sauktas galvas asis, kas iet caur griezuma smaguma centru galvas centrālās inerces asis

2. Šteinera-Haigensa teorēma par asu paralēlo pārnesi

Šteinera-Haigensa teorēma (Šteinera teorēma).
Aksiālais inerces moments pāri I neiznīcināma ass x ir šķērsgriezuma I aksiālā inerces momenta summa no vizuāli paralēlās ass x * , kas iet caur masas šķērsgriezuma centru, un šķērsgriezuma A papildu laukums ir kvadrātā starp abiem. cirvji.

Ja ņem vērā inerces momentus I x і I y x un y asīm, tad asīm ν і u, kas pagrieztas par kut α, ass un smaguma centra inerces momentus aprēķina, izmantojot formulas:

No formulu norādīšanas ir skaidrs, ka

Tobto. aksiālo inerces momentu summa nemainās, griežot savstarpēji perpendikulāras asis, tātad. . Tiek sauktas galvas asis, kas iet caur griezuma smaguma centru galva centrālās asis pererazu. Simetriskiem ass šķērsgriezumiem un simetrijai ar galvas centrālajām asīm. Pārējo asu šķērsgriezuma galvas asu stāvokli nosaka vietējais spіvvіdnoshennia:

de? Inerces momenta asis, tāpat kā galvas asis, sauc galvas inerces momenti:

plus zīme priekšā citam papildinājumam tiek pacelta līdz maksimālajam inerces momentam, mīnusa zīme - līdz minimumam.